Some illustrations of dynamical systems

On 01/07/201801/07/2018 By hpdungIn Geometric topology, Reading-writingLeave a comment

Blog of Gabriel Peyré: https://twitter.com/gabrielpeyre

For example: Gradient flows: https://twitter.com/gabrielpeyre/status/1007865434320850944

The gradient field defines the steepest descent direction. The gradient flow dynamic defines a segmentation of the space into attraction bassins of the local minimizers. pic.twitter.com/wW0flPEWor

— Gabriel Peyré (@gabrielpeyre) 16/6/2018.

The Gaussian curvatures of spheres

On 10/03/201810/03/2018 By hpdungIn Geometric topology, Reading-writingLeave a comment

1. An example of the Gaussian curvature

Example 1 Compute the Gaussian curvature of sphere

$\displaystyle S = \{(x, y, z) \in \mathbb{R}^3 | x^2 + y^2 + z^2 = R^2\}.$

Parametrizing ${X:}$

$\displaystyle U \subset \mathbb{R}^2 \rightarrow S$

$\displaystyle (u, v)\mapsto (u, v, \sqrt{R^2 - u^2 - v^2}).$

we have

$\displaystyle X_u = (1, 0, -\frac{u}{\sqrt{R^2 - u^2 - v^2}}), X_v = (0, 1, -\frac{v}{\sqrt{R^2 - u^2 - v^2}})$

The coefficients of the second fundamental form:

$\displaystyle E = \langle X_u, X_u \rangle = 1 + \frac{u^2}{R^2 - u^2 - v^2}$

$\displaystyle G= \langle X_v, X_v \rangle = 1 + \frac{v^2}{R^2 - u^2 - v^2}$

$\displaystyle F = \langle X_u, X_v \rangle = \frac{uv}{R^2 - u^2 - v^2}$

$\displaystyle \Rightarrow EG - F^2 = (1 + \frac{u^2}{R^2 - u^2 - v^2})(1 + \frac{v^2}{R^2 - u^2 - v^2}) - \frac{u^2v^2}{(R^2 - u^2 - v^2)^2}$

$\displaystyle = 1 + \frac{u^2}{R^2 - u^2 - v^2}+ \frac{v^2}{R^2 - u^2 - v^2}$

$\displaystyle EG - F^2= \frac{R^2}{R^2 - u^2 - v^2}$

we compute coefficients of the first fundamental form:

$\displaystyle N= -\frac{X_u \wedge X_v}{\|X_u \wedge X_v\|}$

$\displaystyle X_u \wedge X_v = (\frac{u}{R^2 - u^2 - v^2}, \frac{v}{R^2 - u^2 - v^2}, 1)$

$\displaystyle \|X_u \wedge X_v\| = \sqrt{\frac{R^2}{R^2 - u^2 - v^2}}$

$\displaystyle = \frac{R}{\sqrt{R^2 - u^2 - v^2}}$

$\displaystyle \Rightarrow N = -\frac{X_u \wedge X_v}{\|X_u \wedge X_v\|} = -(\frac{u}{R}, \frac{v}{R}, \frac{\sqrt{R^2 - u^2 - v^2}}{R})$

$\displaystyle X_{uu} = (0, 0, - \frac{R^2 - v^2}{\sqrt{(R^2 - u^2 - v^2)^3}})$

$\displaystyle X_{vv} = (0, 0, -\frac{R^2-u^2}{\sqrt{(R^2-u^2-v^2)^3}})$

$\displaystyle e = \langle N, X_{uu} \rangle = \frac{v^2 - R^2}{R}\cdot \frac{1}{R^2 - u^2 - v^2}$

$\displaystyle g = \langle N, X_{vv} \rangle = \frac{u^2 - R^2}{R}\cdot \frac{1}{R^2 - u^2 - v^2}$

$\displaystyle f = - \langle N_u, X_v \rangle = \frac{uv}{R(R^2 - u^2 - v^2)}$

where

$\displaystyle N_u = (-\frac{1}{R}, 0, \frac{u}{R\sqrt{R^2 - u^2 - v^2}})$

$\displaystyle X_v = (0, 1, -\frac{v}{\sqrt{R^2 - u^2 - v^2}})$

These imply that

$\displaystyle eg - f^2 = \frac{1}{R^2(R^2 - u^2 - v^2)^2}[(u^2 - R^2)(v^2 - R^2) - u^2v^2]$

$\displaystyle = \frac{1}{R^2(R^2 - u^2 - v^2)^2}[- (u^2 + v^2)R^2 + R^4] = \frac{R^2[R^2 - u^2 - v^2]}{R^2(R^2 - u^2 - v^2)^2}$

$\displaystyle = \frac{1}{R^2 - u^2 - v^2}.$

By the above computation, the curvature of sphere is

$\displaystyle K = \frac{eg - f^2}{EG - F^2} = \frac{1}{R^2}$ .

The \L ojasiewicz exponent at infinity

On 14/05/201719/05/2017 By hpdungIn Reading-writingLeave a comment

The \L ojasiewicz exponent at infinity

References: Paper of Krasinski, On the \L ojasiewicz exponent at infinity of polynomial mappings, Acta. Math. Vietnam. Vol. 32, No. 2-3, 2007.

Definition:

Let ${F = (F_1, \dots, F_m) : \mathbb{C}^n \rightarrow \mathbb{C}^m}$ be a polynomial mapping. The \L ojasiewicz exponent of ${F}$ at infinity is defined as the best exponent ${\nu}$ for which the following inequality holds

$\displaystyle |F(z)| \ge C|z|^\nu,$

for some constant ${C > 0}$ and sufficiently large ${|z|}$ .

$\displaystyle \mathcal{L}_{\infty}(F) := \sup\{\nu \in \mathbb{R}| \exists C >0, R>0 : \forall z \in \mathbb{C}^n, |z| \ge R, |F(z)| \ge C|z|^\nu\}.$

Note that ${\mathcal{L}_{\infty}(F) \in \mathbb{R} \cup \{-\infty\}}$ .

Definition

Let ${F = (F_1, \dots, F_m): \mathbb{C}^n \rightarrow \mathbb{C}^m}$ be a polynomial mapping and ${S \subset \mathbb{C}^n}$ be unbounded set. The \L ojasiewicz exponent of ${F}$ at infinity on ${S}$ is defined as the best exponent ${\nu}$ for which the following inequality holds

$\displaystyle |F(z)| \ge C|z|^\nu$

for some constant ${C > 0}$ and sufficiently large ${|z|}$ in ${S}$ . This exponent is denoted by ${\mathcal{L}_{\infty}(F|S)}$ :

$\displaystyle \mathcal{L}_{\infty}(F|S) :=\sup\{\nu \in \mathbb{R}| \exists C >0, R>0 : \forall z \in S, |z| \ge R, |F(z)| \ge C|z|^\nu\}.$

For example

${F(x,y) = (x, xy-1): \mathbb{C}^2 \rightarrow \mathbb{C}^2.}$

We have ${\mathcal{L}_{\infty}(F) = -1}$ .
And ${\mathcal{L}_{\infty}(F|S) = 0}$ where ${S = \{y = 0\}}$ .

\L ojasiewicz exponent has relationship with properness of mappings

Theorem 1 ${\mathcal{L}_{\infty}(F) > 0}$ if and only if ${F}$ is a proper mapping.

Remark 1 Recall the properness of map. ${F}$ is called proper mapping if ${F}$ sastisfies the following property: ${F^{-1}(K)}$ is a compact set if ${K}$ is a compact set. This fact is equivalent to ${|x| \rightarrow +\infty \Rightarrow |F(x)| \rightarrow +\infty}$ .

On the diffetential of a mapping 2

On 20/06/201620/06/2016 By hpdungIn Geometric topology, Reading-writingLeave a comment

In the case ${\psi : \mathbb{R}^n \rightarrow \mathbb{R}^m}$ case, there is a linear map, which is “linear approximation” of ${\psi}$ . In the manifold case, there is a similar linear map, but now it acts between tangent spaces. If ${M}$ and ${N}$ are smooth manifolds and ${\psi \colon M \rightarrow N}$ is a smooth map then for each ${m \in M}$ , the map

$\displaystyle d\psi \colon T_mM \rightarrow T_{\psi(m)}N$

is defined by

$\displaystyle d\psi(v)(f) = v(f \circ \psi)$

is called the pushforward. Actually,

$\displaystyle d\psi \colon TM \rightarrow TN.$

Suppose that ${\dim{M} \ge \dim{N}}$ and ${f \colon M \rightarrow N}$ is a differentiable mapping. We have

Definition 1 The mapping ${f}$ is called a trivial fibration (differentiable) on ${N}$ if there exists a differential manifold ${F}$ , is called fibre of ${f}$ , and a diffeomorphism

$\displaystyle \phi \colon M \rightarrow N \times F$

such that the following diagram is commutative

Representation of a linear functional

On 17/06/201617/06/2016 By hpdungIn Analysis and Optimization, Reading-writingLeave a comment

We review results of Haviland and Riesz on the reperesentation of a linear functional.

Definition 1 Let ${X}$ be a subset of ${\mathbb{R}^n}$ and ${C(X)}$ be algebra of continuous functions on ${X}$ . A positive linear functional on ${C(X)}$ is a linear functional ${L}$ with ${L(f) \ge 0}$ for all ${f \in C(X)}$ such that ${f(a) \ge 0, \forall a \in X}$ .

We recall Haviland’s result in \cite{Marshall2} (also see \cite{Ha1, Ha2}), with ${\mathbb{R}[x_1, \dots, x_n]}$ denotes the ring of real multivariable polynomials:

Theorem 2 (Haviland) For a linear functional ${L: \mathbb{R}[x_1, \dots, x_n]}$ and closed set ${K}$ in ${\mathbb{R}^n}$ , the following are equivalent:

${L}$ comes from a Borel measure on ${K}$ , i.e., ${\exists}$ a Borel measure ${\mu}$ on ${K}$ such that, ${\forall f \in \mathbb{R}[x_1, \dots, x_n], L(f) = \int f d\mu.}$
${L(f) \ge 0}$ holds for all ${f \in \mathbb{R}[x_1, \dots, x_n]}$ such that ${f \ge 0}$ on ${K}$ .

In Haviland’s theorem, a positive linear functional extended from ring of real multivariable polynomials to larger subalgebra and this theorem can be derived as a consequence of the following Riesz Representation Theorem (see \cite[p. 77]{KS}):

Theorem 3 (Riesz Representation Theorem) Let ${X}$ be a locally compact Hausdorff space and let ${L: C_c(X) \rightarrow \mathbb{R}}$ be a positive linear functional. Then there exists a unique Borel measure ${\mu}$ on ${X}$ such that

$\displaystyle L(f) = \int f d\mu, \forall f \in C_c(X).$

${C_c(X)}$ is the algebra of continuous functions with compact support.

Riesz Representation Theorem – 1

On 01/03/201601/03/2016 By hpdungIn Analysis and Optimization, Reading-writingLeave a comment

This paragraph we follow the book of Rudin [1]. On linear functionals, there is special relationship between integration and linear functionals. In ${L^1(\mu)}$ , a vector space, for any positive measure ${\mu}$ , the mapping

$\displaystyle f \mapsto \int_X f d\mu.$

example, let ${C([0,1])}$ be the set of all continuous functions on the unit interval ${I = [0,1]}$ . Then

$\displaystyle \Lambda f = \int_0^1 f(x)dx \quad \ (f \in C([0,1])),$

has two properties:

${\Lambda(f + g) = \int_0^1[f(x) + g(x)]dx = \int_0^1f(x)dx + \int_0^1g(x)dx = \Lambda(f) + \Lambda(g)}$ .
${\Lambda(c.f) =\int_0^1cf(x)dx = c\int_0^1f(x)dx= c.\Lambda(f)}$ .

so it is a linear functional on ${C([0,1])}$ . Moreover, this is a positive linear functional: if ${f \ge 0}$ then ${\Lambda(f) \ge 0}$ .

Consider a segment ${(a,b) \subset I}$ and the class of all ${f \in C(I)}$ with ${0 \le f(x) \le 1, \forall x \in I}$ and ${f(x) = 0, \forall x \notin (a,b)}$ or support of ${f}$ is ${(a,b) \subset I}$ . So we get ${\Lambda(f) = \int_a^b f(x)dx \le \int_a^bdx = b-a}$ . It is important that the length of ${(a,b)}$ related to the values of the functional ${\Lambda}$ .

There is an important theorem of F. Riesz, this illustrates to above event

Theorem 1 (F. Riesz) Let $X$ be a closed subset of $\mathbb{R}$ . Then every positive linear functional ${\Lambda}$ on ${C(X)}$ there corresponds a finite positive Borel measure ${\mu}$ on ${X}$ such that

$\displaystyle \Lambda(f) = \int_X fd\mu \quad \ (f \in C(X)).$

References

[1] W. Rudin, Real and Complex analysis, Mc.Graw-Hill, 1970.

Classical Lojasiewicz inequalities

On 10/09/201523/09/2015 By hpdungIn Algebraic Geometry, Reading-writingLeave a comment

Let ${f : \mathbb{R}^n \rightarrow \mathbb{R}}$ be a real analytic function with ${f(0) = 0}$ . Let ${V := \{x \in \mathbb{R}^n | f(x) = 0\}}$ and ${K}$ be a compact subset in ${\mathbb{R}^n}$ . Then the (classical) \L ojasiewicz inequality asserts that:

There exist ${c > 0, \alpha > 0}$ such that
$\displaystyle |f(x)| \ge cd(x, V)^\alpha\quad \text{for}\ x \in K.\ \ \ \ \ (1)$

\noindent Let ${f : \mathbb{R}^n \rightarrow \mathbb{R}}$ be a real analytic function with ${f(0) = 0}$ and ${\nabla f(0) = 0}$ . The \L ojasiewicz gradient inequality asserts that:

There exist ${C > 0, \rho \in [0, 1)}$ and a neighbourhood ${U}$ of ${0}$ such that
$\displaystyle \|\nabla f(x)\| \ge C|f(x)|^\rho\quad \text{for}\ x \in U.\ \ \ \ \ (2)$

As a consequence, in (1), the order of zero of an analytic function is finite, and if ${f (x)}$ is close to ${0}$ then ${x}$ is close to the zero set of ${f}$ . However, if ${K}$ is not compact, the latter is not always true and the inequality (1) does not always hold. The inequality (2) is similar to (1), it is not true in the case of $K$ is non-compact.

Two inequalities (1) and (2) have some special cases. For example, in the inequality (1), if ${f}$ has only isolated zero, i.e. ${V = f^{-1}(0) = \{(0, 0, \dots, 0)\}}$ , this implies ${d(x, V) = \|x\|}$ . Hence, we have

$\displaystyle |f(x)| \ge C\|x\|^\alpha, \text{for}\ x\in K.$

On the other hand, being different from (2), we have another inequality:

$\displaystyle \|\nabla f(x)\| \ge c\|x\|^\beta, \text{for}\ x \in U.$

There are some relations between ${\alpha, \beta}$ and ${\rho}$ in complex case and real cases…

On a property of holomorphic functions

On 07/09/201514/10/2015 By hpdungIn Analysis and Optimization, Reading-writingLeave a comment

We can see that a holomorphic functions are the complex functions such that they can express a convergent power series

$\displaystyle f(z) = \sum_{i=0}^\infty a_nz^n.$

We want to compute ${\int\limits_\gamma f(z)dz}$ . Suppose ${\gamma}$ is closed curve (Jordan curve).

We compute the integral for ${\gamma = \mathbb{S}^1}$ . Firstly, consider ${\int_{\mathbb{S}^1}z^ndz, n \ge 1}$ . Change the variables, ${z = e^{2\pi it}, t \in [0,1]}$ , so

$\displaystyle \int_{\mathbb{S}^1}z^ndz = \int_0^1e^{2n\pi it}2 \pi i\cdot e^{2\pi it}dt = \int_0^1e^{2(n+1)\pi it}2 \pi idt = \dfrac{e^{2(n+1)\pi it}}{n+1}\bigg|_0^1 = 0.$

This computation, we think that it is important, because it implies a classical result
Theorem 1 (Cauchy integral theorem) Let ${f : \mathbb{C} \rightarrow \mathbb{C}}$ be a holomorphic function on ${\mathbb{C}}$ . Then

$\displaystyle \int_\gamma f(z) dz= 0,$

with ${\gamma}$ is closed Jordan curve.

Of course it has modulo an any closed Jordan curve: If $\gamma_1$ and $\gamma_2$ are two closed Jordan curve with a common fixed point then $\displaystyle \int_{\gamma_1} f(z)dz = \int_{\gamma_2} f(z) dz,$

Một ví dụ về mặt chính quy

On 04/09/201506/09/2015 By hpdungIn Geometric topology, Reading-writingLeave a comment

BT. Cho hàm $f(x,y,z)=z^{2}$ . CMR $0$ không là giá trị chính qui của hàm $f$ thế nhưng $f^{-1}(0)$ vẫn là mặt chính qui.

Lời giải.

Ta có ma trận $(f_x \ f_y \ f_z) = (0 \ 0 \ 2z)$ suy biến tức $rankA < 1$ khi và chỉ khi $z=0$ , do đó tại điểm $(x, y, 0), \forall x, y \in \mathbb{R}$ , ma trận trên suy biến và do đó là điểm kì dị. Mà $f(x,y,0)=0$ nên $0$ là giá trị tới hạn, hay ko phải giá trị chính qui. Nhưng $f^{-1}(0)$ là mặt phẳng Oxy, đây là mặt trơn nên chính qui.

On the classical moment problems

On 30/08/201508/09/2015 By hpdungIn Analysis and Optimization, Reading-writingLeave a comment

We introduce to the classical moment problem, a short history. We refer to Akhiezer’s book:

N. I, Akhiezer, The Classical Moment Problem and Some Related Questions in
Analysis, Oliver & Boyd, Edinburgh/London, 1965.

and Christiansen’s notes: Moment (on Steven Miller’s page ).

The moment problem is a classical problem in analysis. This problem occurs for the first time in the work of Chebychev in 1873. After that, T.Stieltjes (1894-1895) and A.Markov consider more general case. Chebychev and A.Markov took the moment problem in the relationship with probability theory. The first solution and discussion of extended moment problem is due to Hamburger, he studied Classical moment problem (one-dimensional).
Classical moment problem (one-dimensional) Given an infinite sequence of real numbers ${\{s_n\}_n}$ ( ${s_0 = 1}$ ). Does there exist a positive Borel measure ${\mu}$ such that:

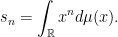
$\displaystyle s_n = \int_{\mathbb{R}}x^nd\mu(x).$

In general, we have Classical moment problem (multidimensional)
Given a function ${s : \mathbb{N}^k \rightarrow \mathbb{R}}$ . Does there exist a positive Borel measure ${\mu}$ such that:

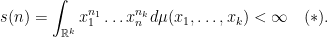
$\displaystyle s(n) = \int_{\mathbb{R}^k}x_1^{n_1}\dots x_n^{n_k}d\mu(x_1,\dots,x_k)<\infty \quad (*).$

In the case one-dimensional moments, the sequence ${\{s_n\}}$ is a function and we have ${s_n = s(n), n \in \mathbb{N}}$ .
Two measure ${\mu}$ and ${\nu}$ are called equivalent if they satisfy:

$\displaystyle s_n = \int_{\mathbb{R}^k}x^n d\mu(x) = \int_{\mathbb{R}^k}x^n d\nu(x).$

In other words, we say they have same moments.
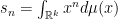The measure ${\mu}$ is called determinate if there only exists ${\mu}$ such that ${s_n = \int_{\mathbb{R}^k}x^n d\mu(x)}$ and indeterminate otherwise.
The aims of the multidimensional moment problem are:

To find necessary and sufficient conditions for existence of measure ${\mu}$ satisfying (*).
To be able to decide determinacy.
In the indeterminate case to give a complete description of all measures satisfying (*).

M	T	W	T	F	S	S
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30	31

Mathematics

Category: Reading-writing