Khai bút

On 31/01/201431/01/2014 By hpdungIn Blog - newsLeave a comment

Gọi là khai bút, thực ra là khai…phím ^_^. Tục khai bút đầu xuân đã có từ lâu đời. Nhà tôi cũng vậy, năm nào đến xuân từ thời cụ tôi cũng khai bút. Và đây là bài thơ mà cụ hay dùng, không rõ tác giả:

Khai bút.

Sang xuân cử bút khai,

Phú quý tự nhiên lai.

Gia đình đa hưng vượng,

Nhật nhật tống tam tai.

Nay tôi cũng dùng lại bài thơ trên. Sang năm mới chúc những người ghé thăm blog này một năm mới an lành, hạnh phúc.

CHÚC MỪNG NĂM MỚI GIÁP NGỌ

On 30/01/2014 By hpdungIn Blog - newsLeave a comment

Viện sĩ người Kazakhtan tiếp cận lời giải của bài toán thiên niên kỷ

On 22/01/2014 By hpdungIn Blog - newsLeave a comment

Đó là giáo sư Otelbaev người Kazakhtan, ông đã đưa ra lời giải cho sự tồn tại các nghiệm dạng mạnh của các phương trình Navier-Stokes, một trong 7 bài toán của thiên niên kỷ do Viện nghiên cứu Clay đưa ra. Mỗi lời giải một trong các bài toán này sẽ được phần thưởng 1 triệu USD. Một bài đã được giải bởi Perelman.

Link: http://bnews.kz/en/news/post/180213/

A nice list of articles of the Mean Value Theorem

On 22/01/201422/01/2014 By hpdungIn Analysis and Optimization, CalculusLeave a comment

A nice list (by John H. Mathews) of articles of various authors on the theme of extending the validity of the Mean Value Theorem to vector values function.

Source: http://mathoverflow.net/questions/80955/mean-value-theorem-for-operators?rq=1

A classical result of Kadec and Pelczynski

On 22/01/201422/01/2014 By hpdungIn Analysis and OptimizationLeave a comment

A question of member of Mathoverflow:

In this question the norm of $L^{P}[0,1]$ is denoted by $\|.\|_p$ .

Let $p$ and $q$ be two arbitrary real numbers with $2<p<q$ .

> Assume that $S$ is a subvector space of $L^{p}[0, 1] \bigcap L^{q}[0, 1]$ such that the identity operator $\text{Id.}: (S, \|.\|_p) \to (S, \|.\|_q)$ is a bounded operator. Does this implies that $S$ is a finite dimensional space?

If I am note mistaken, this is proved for $p=2, q=\infty$ , by Grothendieck.

The answer of Bill Johnson on MO:

In fact, Kadec and Pelczynski proved that a subspace of $L_p$ , $2<p<\infty$, is closed in $L_r$ for some $r<p$ if and only if the subspace is isomorphic to a Hilbert space.

Kadec, M. I.; Pełczyński, A. Bases, lacunary sequences and complemented subspaces in the spaces Lp. Studia Math. 21 1961/1962 161–176.

Thử latex về ma trận trên wordpress

On 21/01/201421/01/2014 By hpdungIn Linear AlgebraLeave a comment

$\bigg(\begin{matrix} 1 & 0\\ 0 & 1 \end{matrix}\bigg)$

An interesting integral: $latex \int_0^\infty e^{-6t}dt$

On 20/01/201421/01/2014 By hpdungIn CalculusLeave a comment

An interesting integral: $\int_0^\infty e^{-6t}dt$ .

This is the problem on Mathematics of Stackexchange.com.

The solution of Dror helps us learn the following trick: $de^y = e^y.dy \Rightarrow dy = \dfrac{de^y}{e^y}$ . So $\int_{-\infty}^xe^{y}dy=\int_{-\infty}^xde^{y}=e^x- \lim_{y \to -\infty}e^y=e^x-0=e^x$ .

Dror’s solution:
So, by substituting $y=-6t$ , we can use this propety. We calculate:
$dt=-\frac{1}{6}dy, 0 \to0,\infty \to - \infty$

The integral then becomes:
$\int_0^\infty e^{-6t}dt=\int_0^{-\infty}-\frac{1}{6}e^{y}dy=\frac{1}{6}\int_{-\infty}^0e^{y}dy=\frac{1}{6}*e^0=\frac{1}{6}*1=\frac{1}{6}$

An example of scalar product

On 12/01/201418/01/2014 By hpdungIn Linear AlgebraLeave a comment

Let $V$ be the space of continous real-valued functions on the interval $[a,b]$ . If $f, g \in V$ , we define

$\langle f, g\rangle = \int\limits_a^b f(x)g(x)dx$

It is easy to prove that this is a scalar product.

If $V$ is the space of continous functions on the interval $[-\pi, \pi]$ . Let $f$ be the function given by $f(x) = \sin{kx}$ , where $k$ is some interger $> 0$ . Then

$\|f\| = \sqrt{\langle f, f \rangle} = \big( \int\limits_{-\pi}^\pi \sin^2{kx}\big)^{1/2} dx = \sqrt{\pi}$ .

If $g$ if a continous function on $[-\pi, \pi]$ then $\langle g, f \rangle = \int\limits_{-\pi}^\pi g(x)\sin{kx} dx$ .

And Fourier coefficient of $g$ with respect to $f$ is $\dfrac{\langle g, f \rangle}{\langle f, f \rangle} = \dfrac{1}{\pi}{\int\limits_{-\pi}^\pi g(x)\sin{kx} dx}$ .

References

[La] Lang. S. Linear Algebra, Springer, 2004.

Minimizing by Ekeland’s Variational Principle.

On 11/01/201411/01/2014 By hpdungIn Analysis and Optimization, Reading-writingLeave a comment

Minimizing by Ekeland’s Variational Principle.

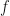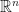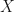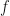Motivation of Ekeland’s paper “On the variational principle.” JMAA, 47. (1974). If $f$ is a continous function on $\mathbb{R}^n$ or Banach space $X$ or complete Riemannian manifold $\overline{M}$ and $f$ has not minimum (of course 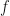$f$ is bounded below) then we can choose a sequence $(x_n)$ such that $f(x_n)$ is “near” to the infimum of $f$ .

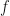We provide following Ekeland’s theorem with 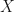$X$ is complete metric space

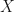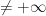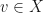Theorem (Ekeland’s Variational Principle). Let $X$ be a complete metric space and $F: X \to \mathbb{R} \cup \{+\infty\}$ a lower semi continous function, $\ne +\infty$ , bounded from below. For every point $u \in X$ satisfying $\inf F \le F(u) \le \inf F + \epsilon$ and every $\lambda > 0$ , there exists some point $v \in X$ such that

$F(v) \le F(u)$ ,

$d(u,v) \le \lambda$ ,

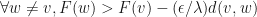$\forall w \ne v, F(w) > F(v) - (\epsilon/\lambda)d(v,w)$ .

In part 5 of the paper, the author states an interesting result on complete Riemannian manifold

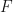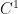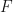Proposition. Let $F$ be a $C^1$ function on a complete Riemannian manifold $\overline{M}$ . If $F$ bounded from below, then, for every $\epsilon \ge 0$ , there exists some point $p_\epsilon \in \overline{M}$ such that

$F(p_\epsilon) \le \inf F + \epsilon^2$ ,

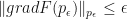$\|gradF(p_\epsilon)\|_{p_\epsilon} \le \epsilon$ .

Conclusion. $p_\epsilon$ is the sequence of minimizer.

Đại số tuyến tính

On 09/01/2014 By hpdungIn Linear AlgebraLeave a comment

Đại số tuyến tính là một nhánh của toán học nghiên cứu các hệ phương trình tuyến tính, ma trận, định thức, không gian vector và các ánh xạ (đồng cấu) tuyến tính giữa các không gian vector. Đây là một lĩnh vực rộng lớn và có ứng dụng vào rất nhiều ngành khác nhau của chính toán học và các khoa học cơ bản cùng với các khoa học ứng dụng khác.